Time and Work - Aptitude test, questions, shortcuts, solved example
Time & Work
Work is always considered as an entire value or one. There exists an analogy between the time-speed-distance problems and work. Work based problems are more or less related to time speed and distance.Important Formulae:
1) Work from days:
If a person can do a work in 'n' days, then person's 1 day work = 1 / n
2) Days from work:
If a person's 1 day work is equal to 1/n , then the person can finish the work in 'n' days.
| 3) Numer of Days = | Total Work |
| Work Done in 1 Day |
Quick Tricks & Tips:
1) Ratio:
If 'A' is 'x' times as good a workman as 'B', then
a) Ratio of work done by A & B in equal time = x: 1
b) Ratio of time taken by A & B to complete the work = 1: x. This means that 'A' takes (1/xth) time as that of 'B' to finish same amount of work.
For example,
if A is twice good a workman as B, then it means that
a) A does twice as much work as done by B in equal time i.e. A:B = 2:1
b) A finishes his work in half the time as B
2) Combined Work:
a) If 'A' and 'B' can finish the work in 'x' & 'y' days respectively, then
| A's one day work = | 1 |
| x |
| B's one day work = | 1 |
| y |
| (A + B)'s one day work = | 1 | + | 1 | = | (x + y) |
| x | y | xy |
| Together, they finish the work in | xy | days. |
| (x + y) |
b) If 'A', 'B' & 'C' can complete the work in x, y & z days respectively, then
| (A + B+ C) 's 1 day work = | 1 | + | 1 | + | 1 | = | (xy + yz + xz) |
| x | y | z | xyz |
| Together, they complete the work in | xyz | days. |
| xy + yz + xz |
c) If A can do a work in 'x' days and if the same amount of work is done by A & B together in 'y' days, then
| A's one day work = | 1 |
| x |
| (A+B)'s one day work = | 1 |
| y |
| B's one day work = | 1 | – | 1 | = | x – y |
| y | x | xy |
| So, 'B' alone will take | xy | days. |
| x – y |
d) If A & B together perform some part of work in 'x' days, B & C together perform it in 'y' days and C & A together perform it in 'z' days, then
| (A + B)'s one day work = | 1 |
| x |
| (B + C)'s one day work = | 1 |
| y |
| (C + A)'s one day work = | 1 |
| z |
| 1 | + | 1 | + | 1 | = 2(A+B+C)'s 1 one day work |
| x | y | z |
| Now, we have at hand (A + B + C)'s one day work = |
| ||||||||||
| 2 | |||||||||||
| (A+ B+ C) will together complete the work in | days | |||||||||
| 2 | ||||||||||
|
If A works alone, then deduct A's work from the total work of B & C to find the time taken by A alone.
For A working alone, time required =A's work - (A+B+C)'s combined work
| = | ||||||||||
| 2 | ||||||||||
|
| = | 2xyz | days |
| [xy + yz – zx] |
Similarly,
| - If B works alone, then time required = | 2xyz |
| (– xy + yz + zx) |
| - If C works alone, then time required = | 2xyz |
| (xy – yz + zx) |
3) Man -Work -Hour related problems:
| Remember that | M D H | = Constant |
| W |
M: Number of Men
D: Number of Days
H: Number of Hours
W: Amount of Work done
If men are fixed, work is proportional to time. If work is fixed , time is inversely proportional to men. Thus,
| M1 x T1 | = | M2 x T2 |
| W1 | W2 |
Once you have understood the following simple things, this chapter will become extremely easy for you.
a) Work and time are directly proportional to each other
b) Number of men and time are inversely proportional to each other
c) And, work can be divided into equal parts i.e. if a task is finished in 10 days, in one day you will finish (1/10th) part of the work.
Questions Variety:
Type 1: Efficiency of two or more workers is give separately. Find how much time would they take to finish the work together.
Examples:
Q 1. Reema can complete a piece of work in 12 days while Seema can the same work in 18 days. If they both work together, then how many days will be required to finish the work?
a. 6 days
b. 7.2 days
c. 9.5 days
d. 12 days
Q 1. Reema can complete a piece of work in 12 days while Seema can the same work in 18 days. If they both work together, then how many days will be required to finish the work?
a. 6 days
b. 7.2 days
c. 9.5 days
d. 12 days
The answer is given below.
Q 2. If 'A' completes a piece of work in 3 days, which 'B' completes it in 5 days and 'C' takes 10 days to complete the same work. How long will they take to complete the work , if they work together?
a. 1.5 days
b. 4.5 days
c. 7 days
d. 9.8 days
a. 1.5 days
b. 4.5 days
c. 7 days
d. 9.8 days
The answer is given below.
Type 2: Find the time required to complete the work
a) by one worker if the total time taken by all workers and one of the workers are given.
b) either alone or together by the workers for the given times of workers in combined form.
a) by one worker if the total time taken by all workers and one of the workers are given.
b) either alone or together by the workers for the given times of workers in combined form.
Examples:
Q 3. Two painters 'P1' & 'P2' paint the bungalow in 3 days. If P1 alone can paint the bungalow in 12 days, in how many days can 'P2'' alone complete the same paint work?
a. 4 days
b. 6 days
c. 9 days
d. 12 days
a. 4 days
b. 6 days
c. 9 days
d. 12 days
The answer is given below.
Q 4. A & B can make paintings in 6 days, B & C can can make those paintings in 10 days. If A, B & C together can finish the work in 4 days, then A & C together will do it in ________ days.
a. 4 (2/7) days
b. 1/ 8 days
c. 2 (2/5) days
d. 6 (3/ 8) days
a. 4 (2/7) days
b. 1/ 8 days
c. 2 (2/5) days
d. 6 (3/ 8) days
The answer is given below.
Type 3: Find the time required
a) to complete the work together if one worker is 'm' times as efficient as the other worker & takes 'D' days less than the other worker
b) to complete the work by one of the workers if they work together or if work efficiencies of two workers are given.
a) to complete the work together if one worker is 'm' times as efficient as the other worker & takes 'D' days less than the other worker
b) to complete the work by one of the workers if they work together or if work efficiencies of two workers are given.
Examples:
Q 5. Pooja is twice as efficient as Aarti and takes 90 days less than Aarti to complete the job. Find the time in which they can finish the job together.
a. 30 days
b. 45 days
c. 60 days
d. 90 days
a. 30 days
b. 45 days
c. 60 days
d. 90 days
The answer is given below.
Q 6. Monika is twice as good as Sonika and together they complete a piece of work in 20 days. In how many days will Monika alone will finish the work?
a. 22 days
b. 30 days
c. 37 days
d. 52 days
a. 22 days
b. 30 days
c. 37 days
d. 52 days
The answer is given below.
Type 4: Calculate the time required by men or (combination of men with other people) to complete a certain work in certain hours for the given another set of number of required men, work & hours.
Examples:
Q 7. 6 men can pack 12 boxes in 7 days by working for 7 hours a day. In how many days can 14 men pack 18 boxes if they work for 9 hours a day?
a. 3.5 days
b. 5 days
c. 7.5 days
d. 12 days
Q 7. 6 men can pack 12 boxes in 7 days by working for 7 hours a day. In how many days can 14 men pack 18 boxes if they work for 9 hours a day?
a. 3.5 days
b. 5 days
c. 7.5 days
d. 12 days
The answer is given below.
Q 8. 4 men and 5 boys can do a piece of work in 20 days while 5 men and 4 boys can do the same work in 16 days. In how many days can 4 men and 3 boys do the same work?
a. 10 days
b. 15 days
c. 20 days
d. 25 days
a. 10 days
b. 15 days
c. 20 days
d. 25 days
The answer is given below.
-----------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------
Ans.1
Correct answer : (b)
Hint:
| A's one day work = | 1 |
| 12 |
| B's one day work = | 1 |
| 18 |
| (A + B)'s one day work = | 1 | + | 1 | = | (18 + 12) | = | 30 | = | 1 |
| 12 | 18 | (12 x 18) | 216 | 7.2 |
Ans.2
Correct answer :(a)
Hint:
| A's one day work = | 1 |
| 3 |
| B's one day work = | 1 |
| 5 |
| C's one day work = | 1 |
| 10 |
| (A+ B+ C)'s one day work = | 1 | + | 1 | + | 1 | = | 1 |
| 3 | 5 | 10 | 1.5 |
Ans.3
Correct answer: (a)
Hint:
| If a person can do a part of work in 'n' days, then person's work in 1 day = | 1 |
| n |
| As painters P1 & P2 paint the bungalows in 3 days, then work done by both painters = | 1 |
| 3 |
| As P1 paint it alone in 12 days, then work done by painter P1 = | 1 |
| 12 |
| Work done by painter P2 = | 1 | – | 1 | = | 4 – 1 | = | 3 | = | 1 |
| 3 | 12 | 12 | 12 | 4 |
Ans.4
Correct answer: (a)
Hint:
We are given that, A,B, & C together complete the work in 4 days.
| We can write, (A+B+C) 's 1 day work = | 1 |
| 4 |
| Similarly, (A+B) 's 1 day work = 1/6 days & (B+C)'s 1 day work = | 1 |
| 10 |
Since the work is divided in combination and we are asked to find out the combined work of (A + C), so we can find out,
(A + C)'s 1 day work = [2 (A+B+C)'s 1 day work] – [(A+ B) 's 1 day work + (B+C)'s 1 day work]
| = |  | 2 x | 1 |  | – | | 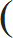 | 1 | 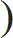 | + | 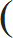| 1 | | |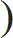
| 4 | 6 | 10 |
| = | 1 | – | 16 | = | 1 | – | 4 | = | 7 |
| 2 | 60 | 2 | 15 | 30 |
| Hence, A & C together can complete the work in 30 /7 days = 4 | 2 | days. |
| 7 |
A.5
Correct answer :(c)
Hint:
Assume that Pooja completes the job in 'x' days.
So, Aarti will take '2x' days to complete the same job.
As Pooja takes 90 days less than Aarti, we get
x = 2x – 90
By solving this equation, we get x = 90 .
Thus, 2x = 2 x 90 = 180
Part of job done by Pooja in 1 day = 1/ 90
Part of job done by Aarti in 1 day = 1/180
(Part of job done together in 1 day) = (Part of job done by Pooja in 1 day) + (Part of job done by Aarti in 1 day)
= (1/90) + (1/180)
= 3/180
=1/60
(1/60)th part of whole job will be completed by Pooja and Aarti together in one day.
Therefore, the whole job will be completed in 60 days together.
Alternate Method: Since 'A' is 'm' times as efficient as 'B' & takes 'D' days less than 'B', then the time required to complete the job together is given by,
| T = m x | D |
| (m2 – 1) |
Ans.6
Correct answer : (b)
Hint: If 'A' is 'x' times as good a workman as 'B', then ratio of work done by A & B = x: 1
Monika's 1 day work : Sonika's 1 day work = 2:1
(Monika's + Sonika's ) 1 day work = 1 /20
Divide 1/20 in the ratio 2:1 ---------( To divide the number 'a' into ratio x & y , we have first part = ax / x + y )
| Therefore, Monika's 1 day work = | 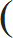| 1 | 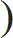| x | 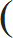| 2 | + 1 | 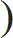| = | 1 |
| 20 | 2 | 30 |
Hence, Monika will alone finish the work in 30 days.
Ans.7
Correct answer :(a)
Hint: If 'w1' work is done by 'm1' men by working for 'h1' hours per day in 'd1' days & 'w2' is work done by men 'm2' working for 'h2' hours per day in 'd2' days, then
| m1d1h1 | = | m2d2h2 |
| w1 | w2 |
| d2 = | m1d1h1w1 |
| m12h2w1 |
| = | 6 x 7 x 7 x 18 |
| 14 x 9 x 12 |
Ans.8
Correct answer:(c)
Hint:
Assume 1 man's 1 day work = x & 1 boy's 1 day work = y
From the given data, we can generate the equations as : 4x + 5y = 1/20 ---(1) & 5x + 4y = 1/16 ---(2)
By solving the simultaneous equations (1) & (2),
x = 1/ 80 & y = 0
| Therefore, (4 men + 3 boys ) 1 day work = 4 x | 1 | + 3 x 0 = | 1 |
| 80 | 20 |
Post a Comment